设满足以下两个条件的有穷数列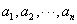 为
为
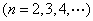 阶“期待数列”:
阶“期待数列”:
① ;②
;② .
.
(1)若等比数列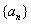 为
为 (
( )阶“期待数列”,求公比
)阶“期待数列”,求公比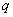 ;
;
(2)若一个等差数列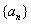 既是
既是 (
( )阶“期待数列”又是递增数列,求该数列的通项公式;
)阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记 阶“期待数列”
阶“期待数列” 的前
的前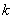 项和为
项和为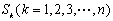 :
:
(ⅰ)求证: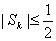 ;
;
(ⅱ)若存在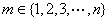 使
使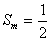 ,试问数列
,试问数列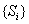 能否为
能否为 阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
推荐套卷
设满足以下两个条件的有穷数列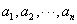 为
为
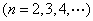 阶“期待数列”:
阶“期待数列”:
① ;②
;② .
.
(1)若等比数列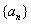 为
为 (
( )阶“期待数列”,求公比
)阶“期待数列”,求公比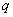 ;
;
(2)若一个等差数列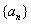 既是
既是 (
( )阶“期待数列”又是递增数列,求该数列的通项公式;
)阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记 阶“期待数列”
阶“期待数列” 的前
的前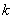 项和为
项和为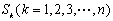 :
:
(ⅰ)求证: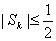 ;
;
(ⅱ)若存在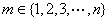 使
使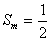 ,试问数列
,试问数列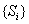 能否为
能否为 阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.