（理）在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC
⊥平面ABC，SA=SC=2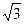
，M、N分别为AB、SB的中点。
（Ⅰ）证明：AC⊥SB；
（Ⅱ）求二面角N-CM-B的大小；
（Ⅲ）求点B到平面CMN的距离．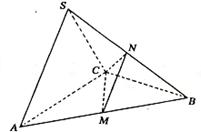
相关试题
．
的图像指出其在
上的单调性．
在
有最大值
和最小值
，求
、
的值。
，集合
，若
，求实数
的取值范围. 
a－3，2a－1，a2 + 1}，a∈R.，当a为何值时，集合A的表示不正确.
满足
且
，数列
的前n项和为
，
是等比数列；
，求证：
。推荐套卷
（理）在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC
⊥平面ABC，SA=SC=2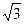，M、N分别为AB、SB的中点。
（Ⅰ）证明：AC⊥SB；
（Ⅱ）求二面角N-CM-B的大小；
（Ⅲ）求点B到平面CMN的距离．
粤公网安备 44130202000953号