如图，在四棱柱ABCD-A1B1C1D1中，已 知平面AA1C1C丄平面ABCD，且AB=BC＝CA=
， AD =" CD" =1
(I)求证：BD丄AA1;
(II)若四边形ACC1A1是菱形，且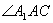
=600，求四棱柱 ABCD-A1B1C1D1的体积.
，
于
，求证：
．
，试确定
的值，使得在此椭圆上存在不同两点关于
对称．
，若
，
成立的
的取值范围．
关于
的表达式；
的值．
，公比为
，前
项和为
，其中最大的一项为
，又它的前
项和为
，求首项
和公比
．推荐套卷
如图，在四棱柱ABCD-A1B1C1D1中，已 知平面AA1C1C丄平面ABCD，且AB=BC＝CA=， AD =" CD" =1
(I)求证：BD丄AA1;
(II)若四边形ACC1A1是菱形，且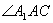=600，求四棱柱 ABCD-A1B1C1D1的体积.
粤公网安备 44130202000953号