在平面直角坐标系内,动圆 过定点
过定点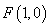 ,且与定直线
,且与定直线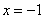 相切.
相切.
(1)求动圆圆心 的轨迹
的轨迹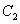 的方程;
的方程;
(2)中心在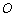 的椭圆
的椭圆 的一个焦点为
的一个焦点为 ,直线过点
,直线过点 .若坐标原点
.若坐标原点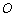 关于直线的对称点
关于直线的对称点 在曲线
在曲线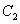 上,且直线与椭圆
上,且直线与椭圆 有公共点,求椭圆
有公共点,求椭圆 的长轴长取得最小值时的椭圆方程.
的长轴长取得最小值时的椭圆方程.
推荐套卷
在平面直角坐标系内,动圆 过定点
过定点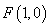 ,且与定直线
,且与定直线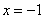 相切.
相切.
(1)求动圆圆心 的轨迹
的轨迹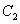 的方程;
的方程;
(2)中心在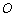 的椭圆
的椭圆 的一个焦点为
的一个焦点为 ,直线过点
,直线过点 .若坐标原点
.若坐标原点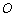 关于直线的对称点
关于直线的对称点 在曲线
在曲线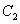 上,且直线与椭圆
上,且直线与椭圆 有公共点,求椭圆
有公共点,求椭圆 的长轴长取得最小值时的椭圆方程.
的长轴长取得最小值时的椭圆方程.