某商家举办购物抽奖活动,盒中有大小相同的9张卡片,其中三张标有数字1,两张标有数字0,四张标有数字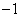 ,先从中任取三张卡片,将卡片上的数字相加,设数字和为
,先从中任取三张卡片,将卡片上的数字相加,设数字和为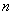 ,当
,当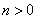 时,奖励奖金
时,奖励奖金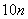 元;当
元;当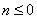 时,无奖励.
时,无奖励.
(1)求取出的三个数字中恰有一个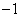 的概率.
的概率.
(2)设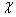 为奖金金额,求
为奖金金额,求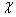 的分布列和期望.
的分布列和期望.
推荐套卷
某商家举办购物抽奖活动,盒中有大小相同的9张卡片,其中三张标有数字1,两张标有数字0,四张标有数字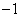 ,先从中任取三张卡片,将卡片上的数字相加,设数字和为
,先从中任取三张卡片,将卡片上的数字相加,设数字和为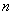 ,当
,当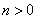 时,奖励奖金
时,奖励奖金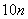 元;当
元;当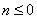 时,无奖励.
时,无奖励.
(1)求取出的三个数字中恰有一个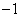 的概率.
的概率.
(2)设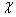 为奖金金额,求
为奖金金额,求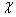 的分布列和期望.
的分布列和期望.