(文科只做(1)(2)问,理科全做)
设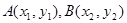 是函数
是函数 图象上任意两点,且
图象上任意两点,且 ,已知点
,已知点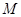 的横坐标为
的横坐标为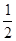 ,且有
,且有 ,其中
,其中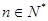 且n≥2,
且n≥2,
(1) 求点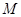 的纵坐标值;
的纵坐标值;
(2) 求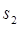 ,
,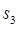 ,
,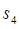 及
及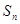 ;
;
(3)已知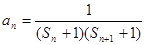 ,其中
,其中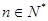 ,且
,且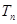 为数列
为数列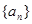 的前n项和,若
的前n项和,若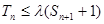 对一切
对一切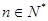 都成立,试求λ的最小正整数值。
都成立,试求λ的最小正整数值。
推荐套卷
(文科只做(1)(2)问,理科全做)
设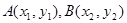 是函数
是函数 图象上任意两点,且
图象上任意两点,且 ,已知点
,已知点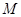 的横坐标为
的横坐标为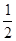 ,且有
,且有 ,其中
,其中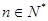 且n≥2,
且n≥2,
(1) 求点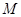 的纵坐标值;
的纵坐标值;
(2) 求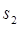 ,
,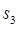 ,
,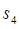 及
及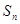 ;
;
(3)已知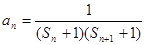 ,其中
,其中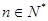 ,且
,且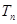 为数列
为数列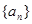 的前n项和,若
的前n项和,若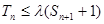 对一切
对一切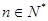 都成立,试求λ的最小正整数值。
都成立,试求λ的最小正整数值。