利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?
(1)如图,一个边长为1的正方形,依次取正方形面积的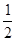 、
、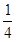 、
、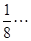
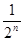 ,根据图示我们可以知道:
,根据图示我们可以知道: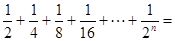 .
.
利用上述公式计算: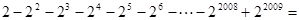 .
.
(2)计算: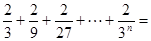 ;
;
(3)计算: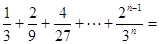 .
.
相关知识点
推荐套卷
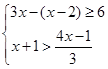
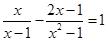
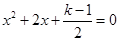 有两个不相等的实数根,k为正整数.
有两个不相等的实数根,k为正整数.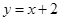 与关于x的二次函数
与关于x的二次函数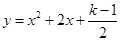 的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值及此时点M的坐标;
的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值及此时点M的坐标;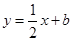 与该新图象恰好有三个公共点,求b的值.
与该新图象恰好有三个公共点,求b的值.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号