已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题: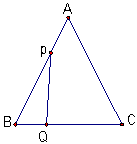
(1)求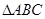 的面积;
的面积;
(2)当t为何值是,△PBQ是直角三角形?
(3)设四边形APQC的面积为y(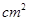 ),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是
),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是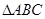 面积的三分之二?如果存在,求出t的值;不存在请说明理由.
面积的三分之二?如果存在,求出t的值;不存在请说明理由.
相关知识点
推荐套卷
 中,
中, 是
是 边上的一点,
边上的一点, 是
是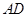 的中点,过点
的中点,过点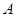 作
作 的延长线于
的延长线于 ,且
,且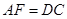 ,连接
,连接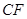 .
.
 ,试猜测四边形
,试猜测四边形 的形状,并证明你的结论.
的形状,并证明你的结论.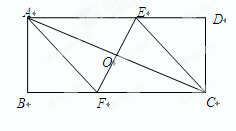
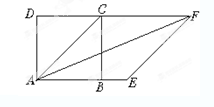
 中,点
中,点 、
、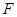 分别在
分别在 、
、 上,
上, 为等腰直角三角形,
为等腰直角三角形, 求
求

 粤公网安备 44130202000953号
粤公网安备 44130202000953号