如图，在直角坐标系中，点D在y轴上，四边形ABCD是等腰梯形，AB∥CD。已知， DO⊥AB， OE⊥BC，E、O分别为垂足，BC="BO" ，O为坐标原点。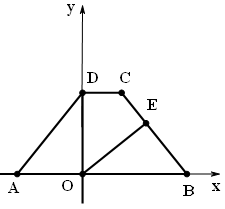
(1) 求证：DO=EO
(2) 已知：C点坐标为（4 ， 8），
①求等腰梯形ABCD的腰长；
②问题探究：在这个坐标平面内是否存在点F，使以点F、D、O、E为顶点的四边形是菱形？若存在，请求出所有符合要求的F点的坐标，并说明理由；若不存在，请说明理由。
相关试题
如图，C为线段BD上一动点,分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC.已知AB=5，DE=1，BD=8，设CD=x.
用含x的代数式表示AC＋CE的长
请问点C满足什么条件时，AC＋CE的值最小?
根据（2）中的规律和结论，请构图求出代数式
的最小值.
如图，正方形OABC的面积为9，点O为坐标原点，点B在函数
（k＞0，x＞0）的图象上，点P（m、n）是函数（k＞0，x＞0）图象上的一个动点，过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设两个四边形OEPF和OABC不重合部分的面积之和为S.
求B点坐标和k的值
当S＝时，求点P的坐标
的图象过P点；
，求
的值.相关知识点
推荐套卷
粤公网安备 44130202000953号