如图，四棱锥P－ABCD中，PA⊥底面ABCD，四边形ABCD中，AB⊥AD，AB＋AD＝4，CD＝
，∠CDA＝45°.
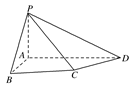
(Ⅰ)求证：平面PAB⊥平面PAD；
(Ⅱ)设AB＝AP．
(ⅰ) 若直线PB与平面PCD所成的角为30°，求线段AB的长；
(ⅱ) 在线段AD上是否存在一个点G，使得点G到点P，B，C，D的距离都相等？说明理由．
相关试题
的离心率为
，长轴长为
，直线
交椭圆于不同的
两点.
是坐标原点，求
面积的最大值.
中
,
边上的中线
所在直线方程为
,
的平分线方程
为
.
的坐标；
的方程.
轴相切，圆心在直线
上，且被直线
截得的弦长为
的圆的方程．
经过直线
的交点，且点
到直线
为实数，函数
. 
，求
的取值范围； 
的最小值； 
，直接写出（不需给出演算步骤）不等式
的解集.推荐套卷
如图，四棱锥P－ABCD中，PA⊥底面ABCD，四边形ABCD中，AB⊥AD，AB＋AD＝4，CD＝，∠CDA＝45°.
(Ⅰ)求证：平面PAB⊥平面PAD；
(Ⅱ)设AB＝AP．
(ⅰ) 若直线PB与平面PCD所成的角为30°，求线段AB的长；
(ⅱ) 在线段AD上是否存在一个点G，使得点G到点P，B，C，D的距离都相等？说明理由．
粤公网安备 44130202000953号