定义在R上的函数f(x)是最小正周期为2的奇函数, 且当x∈(0, 1)时, f (x)＝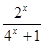
.
（1）求f (x)在[－1, 1]上的解析式;
（2）证明f (x)在(—1, 0)上时减函数;
（3）当λ取何值时, 不等式f (x)＞λ在R上有解?
；
；
在
时取得极值，且
．
（
且
）；
（
且
）；相关知识点
推荐套卷
定义在R上的函数f(x)是最小正周期为2的奇函数, 且当x∈(0, 1)时, f (x)＝.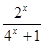
（1）求f (x)在[－1, 1]上的解析式;
（2）证明f (x)在(—1, 0)上时减函数;
（3）当λ取何值时, 不等式f (x)＞λ在R上有解?
粤公网安备 44130202000953号