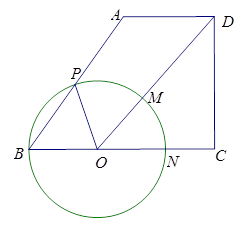
如图,在梯形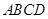 中
中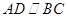 ,
,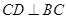 ,已知
,已知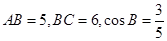 ,点
,点 为
为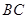 边上的动点,连接
边上的动点,连接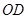 ,以
,以 为圆心,
为圆心, 为半径的⊙
为半径的⊙ 分别交射线
分别交射线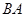 于点
于点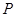 ,交射线
,交射线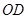 于点
于点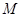 ,交射线
,交射线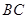 于
于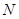 ,连接
,连接 .
.
(1)求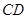 的长.
的长.
(2)当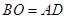 时,求
时,求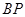 的长.
的长.
(3)在点 的运动过程中,
的运动过程中,
①当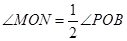 时,求⊙
时,求⊙ 的半径.
的半径.
②当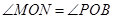 时,求⊙
时,求⊙ 的半径(直接写出答案).
的半径(直接写出答案).
推荐套卷
如图,在梯形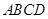 中
中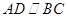 ,
,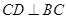 ,已知
,已知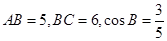 ,点
,点 为
为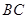 边上的动点,连接
边上的动点,连接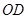 ,以
,以 为圆心,
为圆心, 为半径的⊙
为半径的⊙ 分别交射线
分别交射线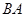 于点
于点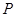 ,交射线
,交射线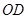 于点
于点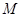 ,交射线
,交射线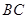 于
于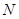 ,连接
,连接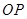 .
.
(1)求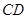 的长.
的长.
(2)当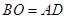 时,求
时,求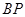 的长.
的长.
(3)在点 的运动过程中,
的运动过程中,
①当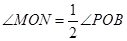 时,求⊙
时,求⊙ 的半径.
的半径.
②当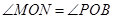 时,求⊙
时,求⊙ 的半径(直接写出答案).
的半径(直接写出答案).