已知:如图,正比例函数y=ax的图象与反比例函数y=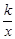 的图象交于点A(3,2).
的图象交于点A(3,2).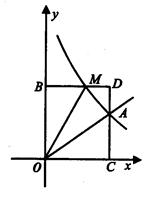
(1)确定上述正比例函数和反比例函数的表达式
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)M(m,n)是反比例函数图象上的一个动点,其中0<m<3,过点M作直线MB//x轴,交y轴于点B;过点A作直线AC//y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为3时,请判断线段BM与DM有何数量关系,并说明理由.
相关知识点
推荐套卷
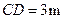 ,标杆与旗杆的水平距离
,标杆与旗杆的水平距离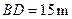 ,人的眼睛与地面的高度
,人的眼睛与地面的高度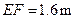 ,人与标杆
,人与标杆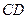 的水平距离
的水平距离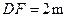 ,求旗杆
,求旗杆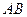 的高度.
的高度.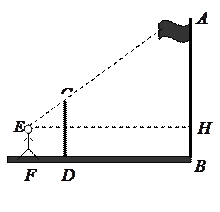
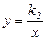 的图象交于A(1,4)、B(3,m)两点。
的图象交于A(1,4)、B(3,m)两点。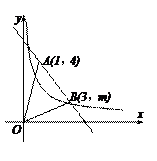
 市的房价平均每年涨价百分之几?
市的房价平均每年涨价百分之几?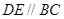 ,
,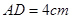 ,
,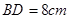 ,
,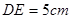 ,求线段
,求线段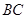 的长.
的长.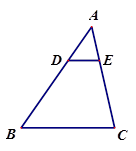
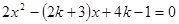 的一个根,求方程的另一个根及
的一个根,求方程的另一个根及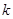 值.
值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号