如图，抛物线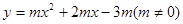
的顶点为H，与
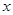轴交于A、B两点（B点在A点右侧），点H、B关于直线：
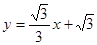对称，过点B作直线BK∥AH交直线于K点．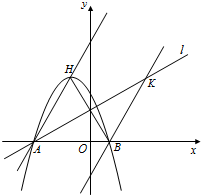
（1）求A、B两点坐标，并证明点A在直线上；
（2）求此抛物线的解析式；
（3）将此抛物线向上平移，当抛物线经过K点时，设顶点为N，求出NK的长．
相关试题
+（-
）
（4）-
ABCD，E，F是对角线BD所在直线上的两点，且AE∥CF，求证：CE∥AF．
ABCD，E， F是对角线BD上的两点，且DE=BF.
相关知识点
推荐套卷
如图，抛物线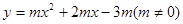的顶点为H，与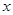轴交于A、B两点（B点在A点右侧），点H、B关于直线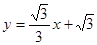：对称，过点B作直线BK∥AH交直线于K点．
（1）求A、B两点坐标，并证明点A在直线上；
（2）求此抛物线的解析式；
（3）将此抛物线向上平移，当抛物线经过K点时，设顶点为N，求出NK的长．
粤公网安备 44130202000953号