假设关于某设备使用年限x（年）和所支出的维修费用y（万元）有如下统计资料：若由资料知，y对x呈线性相关关系，试求：
 |
2 |
3 |
4 |
5 |
6 |
 |
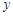2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
（1）回归直线方程；（2）估计使用年限为10年时，维修费用约是多少？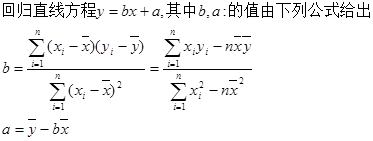
．
B，试求k的取值范围．
在
上有最大值
，试确定常数
，并求这个函数在该闭区间上的最小值。
在区间
上的最大值和最小值。
，
的值域。
，
的最大值和最小值。推荐套卷
假设关于某设备使用年限x（年）和所支出的维修费用y（万元）有如下统计资料：若由资料知，y对x呈线性相关关系，试求：
|
2 |
3 |
4 |
5 |
6 |
|
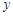2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
（1）回归直线方程；（2）估计使用年限为10年时，维修费用约是多少？．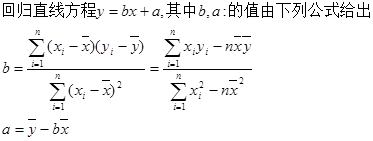
粤公网安备 44130202000953号