动圆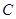 过定点
过定点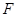
 ,且与直线
,且与直线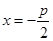 相切,其中
相切,其中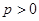 .设圆心
.设圆心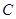 的轨迹
的轨迹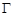 的程为
的程为
(1)求 ;
;
(2)曲线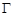 上的一定点
上的一定点 (
(
 0) ,方向向量
0) ,方向向量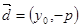 的直线
的直线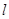 (不过P点)与曲线
(不过P点)与曲线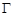 交与A、B两点,设直线PA、PB斜率分别为
交与A、B两点,设直线PA、PB斜率分别为 ,
, ,计算
,计算 ;
;
(3)曲线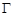 上的两个定点
上的两个定点 、
、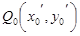 ,分别过点
,分别过点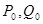 作倾斜角互补的两条直线
作倾斜角互补的两条直线 分别与曲线
分别与曲线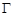 交于
交于 两点,求证直线
两点,求证直线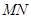 的斜率为定值;
的斜率为定值;
推荐套卷
动圆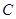 过定点
过定点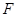
 ,且与直线
,且与直线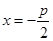 相切,其中
相切,其中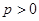 .设圆心
.设圆心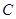 的轨迹
的轨迹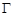 的程为
的程为
(1)求 ;
;
(2)曲线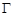 上的一定点
上的一定点 (
(
 0) ,方向向量
0) ,方向向量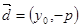 的直线
的直线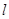 (不过P点)与曲线
(不过P点)与曲线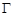 交与A、B两点,设直线PA、PB斜率分别为
交与A、B两点,设直线PA、PB斜率分别为 ,
, ,计算
,计算 ;
;
(3)曲线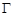 上的两个定点
上的两个定点 、
、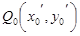 ,分别过点
,分别过点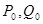 作倾斜角互补的两条直线
作倾斜角互补的两条直线 分别与曲线
分别与曲线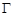 交于
交于 两点,求证直线
两点,求证直线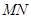 的斜率为定值;
的斜率为定值;