钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为12海里(即MC=12海里).在A点测得岛屿的西端点M在点A的东北方向;航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东60°方向,(其中N,M,C在同一条直线上如图),求钓鱼岛东西两端点MN之间的距离. 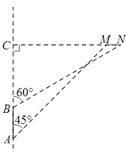
相关知识点
推荐套卷
钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为12海里(即MC=12海里).在A点测得岛屿的西端点M在点A的东北方向;航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东60°方向,(其中N,M,C在同一条直线上如图),求钓鱼岛东西两端点MN之间的距离. 