甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量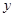 (件)与时间
(件)与时间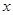 (时)的函数图象如图所示.
(时)的函数图象如图所示.
(1)求甲组加工零件的数量y与时间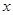 之间的函数关系式.
之间的函数关系式.
(2)求乙组加工零件总量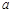 的值.
的值.
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?
相关知识点
推荐套卷
甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量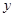 (件)与时间
(件)与时间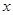 (时)的函数图象如图所示.
(时)的函数图象如图所示.
(1)求甲组加工零件的数量y与时间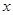 之间的函数关系式.
之间的函数关系式.
(2)求乙组加工零件总量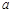 的值.
的值.
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?