如图1，在平面直角坐标系中，A（a，0），B（b，0），C（－1，2），且
．
（1）求a，b的值；
（2）①在x轴的正半轴上存在一点M，使△COM的面积＝
△ABC的面积，求出点M的坐标；
②在坐标轴的其它位置是否存在点M，使△COM的面积＝△ABC的面积仍然成立，若存在，请直接写出符合条件的点M的坐标；
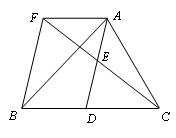
（3）如图2，过点C作CD⊥y轴交y轴于点D，点P为线段CD延长线上一动点，连接OP，OE平分∠AOP，OF⊥OE．当点P运动时，
的值是否会改变？若不变，求其值；若改变，说明理由．
相关试题
有5张形状、大小和质地都相同的卡片，正面分别写有字母：A，B，C，D，E和一个等式，背面完全一致．现将5张卡片分成两堆，第一堆：A，B，C；第二堆：D，E，并从第一堆中抽出第一张卡片，再从第二堆中抽出第二张卡片，背面向上洗匀．
（1）请用画树形图或列表法表示出所有可能结果；（卡片可用A，B，C，D，E表示）
（2）将“第一张卡片上x的值是第二张卡片中方程的解”记作事件M，求事件M的概率．
为了解某校九年级学生体育测试成绩情况，现从中随机抽取部分学生的体育成绩统计如下，其中右侧扇形统计图中的圆心角α为36°．
根据上面提供的信息，回答下列问题：
(1)m=；抽取部分学生体育成绩的中位数为分；
(2)已知该校九年级共有500名学生，如果体育成绩达33分以上(含33分)为优秀，请估计该校九年级学生体育成绩达到优秀的总人数．
如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于F，且AF=BD，连接BF．
（1）求证：BD=CD．
（2）如果AB=AC，试判断四边形AFBD的形状，并证明你的结论．
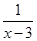=2+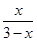
(2) 解不等式组：
)－1－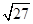
+(5－π)0（2）(2x－1)2+(x－2)(x+2)－4x(x－
)相关知识点
推荐套卷
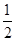粤公网安备 44130202000953号