正方形ABCD中,点O是对角线AC的中点,点P是对角线AC上一动点.
(1)如图1,当点P在线段OA上运动时(不与点A、O重合) ,PE⊥PB交线段CD于点E,PF⊥CD于点E.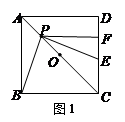
①判断线段DF、EF的数量关系,并说明理由;
②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;
(2)如图2,当点P在线段OC上运动时(不与点O、C重合),PE⊥PB交直线CD于点E,PF⊥CD于点E.判断(1)中的结论①、②是否成立?若成立,说明理由;若不成立,写出相应的结论并证明.
推荐套卷
正方形ABCD中,点O是对角线AC的中点,点P是对角线AC上一动点.
(1)如图1,当点P在线段OA上运动时(不与点A、O重合) ,PE⊥PB交线段CD于点E,PF⊥CD于点E.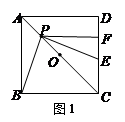
①判断线段DF、EF的数量关系,并说明理由;
②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;
(2)如图2,当点P在线段OC上运动时(不与点O、C重合),PE⊥PB交直线CD于点E,PF⊥CD于点E.判断(1)中的结论①、②是否成立?若成立,说明理由;若不成立,写出相应的结论并证明.