校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.九台三十一中学九年一班数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道上确定点D,使CD与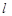 垂直,测得CD长等于18米,在上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
垂直,测得CD长等于18米,在上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.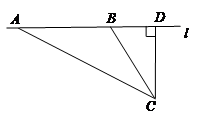
(1) 求AB的长(精确到0.1米,参考数据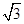 =1.73,
=1.73, =1.41);
=1.41);
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.
相关知识点
推荐套卷
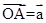 ,试用
,试用 表示
表示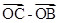 (直接写出答案)
(直接写出答案) ,其中
,其中 .
. ,点
,点 粤公网安备 44130202000953号
粤公网安备 44130202000953号