(1)设椭圆 :
: 与双曲线
与双曲线 :
: 有相同的焦点
有相同的焦点 ,
, 是椭圆
是椭圆 与双曲线
与双曲线 的公共点,且
的公共点,且 的周长为
的周长为 ,求椭圆
,求椭圆 的方程;
的方程;
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.
(2)如图,已知“盾圆 ”的方程为
”的方程为 .设“盾圆
.设“盾圆 ”上的任意一点
”上的任意一点 到
到 的距离为
的距离为 ,
, 到直线
到直线 的距离为
的距离为 ,求证:
,求证: 为定值;
为定值;
(3)由抛物线弧 :
: (
( )与第(1)小题椭圆弧
)与第(1)小题椭圆弧 :
: (
( )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆 ”.设过点
”.设过点 的直线与“盾圆
的直线与“盾圆 ”交于
”交于 两点,
两点, ,
, 且
且 (
( ),试用
),试用 表示
表示 ;并求
;并求 的取值范围.
的取值范围.
推荐套卷
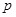 :方程
:方程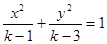 表示双曲线,
表示双曲线, :不等式
:不等式 对一切
对一切 恒成立,若
恒成立,若 为真命题,求
为真命题,求 的取值范围.
的取值范围.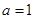 时,求函数
时,求函数 在
在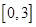 上的值域;
上的值域; 为定义在
为定义在 上的偶函数,求
上的偶函数,求 的值;
的值; 的定义域为
的定义域为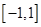 ,值域为
,值域为 ?
? 的函数
的函数 是奇函数。
是奇函数。 的值;
的值; ,不等式
,不等式 恒成立,求
恒成立,求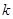 的取值范围;
的取值范围;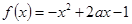 ,若
,若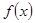 在
在 上的最大值为
上的最大值为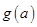 ,求
,求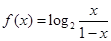 .
. 是增函数.
是增函数. 粤公网安备 44130202000953号
粤公网安备 44130202000953号