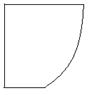
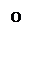学校为扩大规模，把后山一块不规则的非农业用地规划建成一个矩形运动场地．已知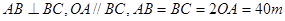
，曲线段
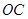是以点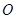
为顶点且开口向上的抛物线的一段（如图所示）．如果要使矩形的相邻两边分别落在
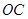上，且一个顶点落在曲线段上，问应如何规划才能使运动场地面积最大？
相关试题
，
求
的值。
中，
。求
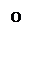
推荐套卷
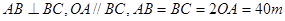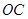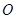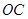学校为扩大规模，把后山一块不规则的非农业用地规划建成一个矩形运动场地．已知，曲线段是以点为顶点且开口向上的抛物线的一段（如图所示）．如果要使矩形的相邻两边分别落在上，且一个顶点落在曲线段上，问应如何规划才能使运动场地面积最大？
粤公网安备 44130202000953号