如图，正方体ABCD—A1B1C1D1棱长为8，E、F分别为AD1，CD1中点，G、H分别为棱DA，DC上动点，且EH⊥FG．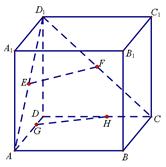
（1）求GH长的取值范围；
（2）当GH取得最小值时，求证：EH与FG共面；并求出此时EH与FG的交点P到直线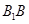
的距离.
＜0}，B＝{x｜x2＋ax＋b≤0}，A∩B＝
，
.
，
，求A∩B，A∪B，
。
．①当
时，求函数
的定义域；
，试求
的取值范围．
：
,在曲线
求一点，使它到直线
：
的距离最小，并求出该点坐标和最小距离.
在二阶矩阵
的作用下变换为曲线
，①求实数
的值；②求
的逆矩阵
.推荐套卷
如图，正方体ABCD—A1B1C1D1棱长为8，E、F分别为AD1，CD1中点，G、H分别为棱DA，DC上动点，且EH⊥FG．
（1）求GH长的取值范围；
（2）当GH取得最小值时，求证：EH与FG共面；并求出此时EH与FG的交点P到直线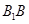的距离.
粤公网安备 44130202000953号