某地政府鉴于某种日常食品价格增长过快，欲将这种食品价格控制在适当范围内，决定对这种食品生产厂家提供政府补贴，设这种食品的市场价格为
元/千克，政府补贴为
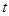元/千克，根据市场调查，当
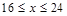时，这种食品市场日供应量
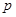万千克与市场日需量
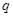万千克近似地满足关系:
，
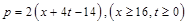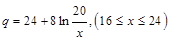。当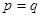
市场价格称为市场平衡价格。
（1）将政府补贴表示为市场平衡价格的函数，并求出函数的值域；
（2）为使市场平衡价格不高于每千克20元，政府补贴至少为每千克多少元？
相关试题
在
轴右边，
的距离减去它到
的直线
与曲线Ｃ有两个交点
，且
，求直线
的斜率.
，函数
.
时，
恒成立，求实数
的最大值.
及其前
项和
满足：
（
，
）.
，
是等差数列；（2）求
及
.
，
，设函数
，（
，且
为常数）
为任意实数，求
的最小正周期；
上的最大值与最小值之和为
，求
．
时，求
在
最小值；
的取值范围；
（
）．推荐套卷
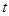某地政府鉴于某种日常食品价格增长过快，欲将这种食品价格控制在适当范围内，决定对这种食品生产厂家提供政府补贴，设这种食品的市场价格为元/千克，政府补贴为元/千克，根据市场调查，当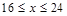时，这种食品市场日供应量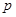万千克与市场日需量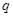万千克近似地满足关系: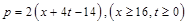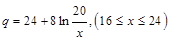，。当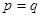市场价格称为市场平衡价格。
（1）将政府补贴表示为市场平衡价格的函数，并求出函数的值域；
（2）为使市场平衡价格不高于每千克20元，政府补贴至少为每千克多少元？
粤公网安备 44130202000953号