（本题共9分）如图，在△ACB中，∠AC
B = 90°，AC = 4，BC =
2，点P为线段CA（不包括端点）上的一个动点，以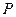
为圆心，1为半径作
．
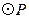（1）连结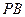
，若
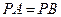，试判断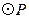与直线AB的位置关系，并说明理由；
（2）当线段PC等于多少时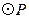，与直线AB相切？
(3)当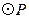与直线AB相交时，写出线段PC的取值范围。
（第（3）问直接给出结果，不需要解题过程）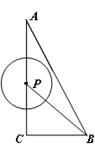
相关试题
的单调区间.
存在单调递减区间，求
的取值范围；
时，求证
成立；
为奇函数，且过点
，函数
．
的解析式并求其定义域；
时不等式
恒成立，求实数a的取值范围．
的定义域；相关知识点
推荐套卷
（本题共9分）如图，在△ACB中，∠ACB = 90°，AC = 4，BC = 2，点P为线段CA（不包括端点）上的一个动点，以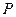为圆心，1为半径作．
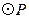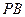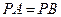（1）连结，若，试判断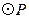与直线AB的位置关系，并说明理由；
（2）当线段PC等于多少时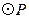，与直线AB相切？
(3)当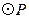与直线AB相交时，写出线段PC的取值范围。
（第（3）问直接给出结果，不需要解题过程）
粤公网安备 44130202000953号