在小学我们知道“三角形的内角和等于 ”,现在把一块含
”,现在把一块含 角的直角三角板
角的直角三角板 的直角顶点
的直角顶点 放置在水平线
放置在水平线 上,如图所示.
上,如图所示.
(1)填空: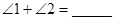 度;
度;
(2) 若把三角板 绕着点
绕着点 按逆时针方向旋转,
按逆时针方向旋转,
①填空:当 = 度时,
= 度时, ∥
∥ .
.
理由: .
②在三角板 绕着点
绕着点 按逆时针方向旋转的过程中,作
按逆时针方向旋转的过程中,作 于点
于点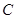 ,
,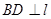 于点
于点 ,图中是否存在相等的角(图中所有的直角相等不加以考虑,不能再随意添加字母或作出其它线条)?若有,试找出图中所有相等的角,并说明理由;若无,请举例说明.
,图中是否存在相等的角(图中所有的直角相等不加以考虑,不能再随意添加字母或作出其它线条)?若有,试找出图中所有相等的角,并说明理由;若无,请举例说明. 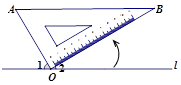
相关知识点
推荐套卷

 ,求
,求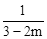 的值;
的值;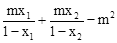 的最大值.
的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号