如图线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.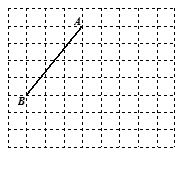
⑴请你在所给的网格中画出线段AC及点B经过的路径;
⑵若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),点B的坐标为(-2, -1),则点C的坐标为 ;
⑶线段AB在旋转到线段AC的过程中,线段AB扫过的区域的面积为 ;
⑷若有一张与⑶中所说的区域形状相同的纸片,将它围成一个几何体的侧面,则该几何体底面圆的半径长为 .
相关知识点
推荐套卷


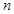 个图形要用块黑色正方形;
个图形要用块黑色正方形;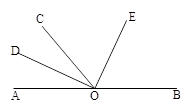
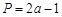 ,
,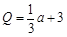 ,且
,且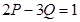 ,求
,求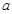 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号