已知函数 满足:对于任意实数
满足:对于任意实数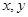 ,都有
,都有 恒成立,且当
恒成立,且当 时,
时,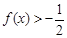 恒成立;
恒成立;
(1)求 的值,并例举满足题设条件的一个特殊的具体函数;
的值,并例举满足题设条件的一个特殊的具体函数;
(2)判定函数 在R上的单调性,并加以证明;
在R上的单调性,并加以证明;
(3)若函数 (其中
(其中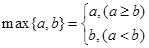 )有三个零点
)有三个零点 ,求
,求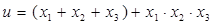 的取值范围.
的取值范围.
推荐套卷
已知函数 满足:对于任意实数
满足:对于任意实数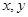 ,都有
,都有 恒成立,且当
恒成立,且当 时,
时,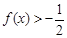 恒成立;
恒成立;
(1)求 的值,并例举满足题设条件的一个特殊的具体函数;
的值,并例举满足题设条件的一个特殊的具体函数;
(2)判定函数 在R上的单调性,并加以证明;
在R上的单调性,并加以证明;
(3)若函数 (其中
(其中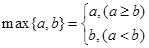 )有三个零点
)有三个零点 ,求
,求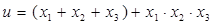 的取值范围.
的取值范围.