本题为选项做题，从甲、乙两题中选做一题即可，如果两题都做，只以甲题计分．
甲：直线l：y=（m﹣3）x+n﹣2（m，n为常数）的图象如图1所示，化简：|m﹣n|﹣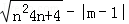
；
乙：已知：如图2，在边长为a的正方形ABCD中，M是边AD的中点，能否在边AB上找到点N（不含A、B），使得△MAN相似？若能，请给出证明；若不能，请说明理由．
时，老师告诉同学们正确的解是
，小明由于看错了系数c，因而得到的解为
，试求a+b+c的值．
的解相同，求a，b的值．
相关知识点
推荐套卷
本题为选项做题，从甲、乙两题中选做一题即可，如果两题都做，只以甲题计分．
甲：直线l：y=（m﹣3）x+n﹣2（m，n为常数）的图象如图1所示，化简：|m﹣n|﹣；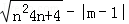
乙：已知：如图2，在边长为a的正方形ABCD中，M是边AD的中点，能否在边AB上找到点N（不含A、B），使得△MAN相似？若能，请给出证明；若不能，请说明理由．
粤公网安备 44130202000953号