已知⊙O1经过 ,
, ,
, ,
, 四点,一次函数
四点,一次函数 的图象是直线
的图象是直线 ,直线
,直线 与
与 轴交于点
轴交于点 .
.
(1)在如图的平面直角坐标系中画出直线l,则直线 与⊙O1的交点坐标为 _______________ ;
与⊙O1的交点坐标为 _______________ ;
(2)若⊙O1上存在整点 (横坐标与纵坐标均为整数的点称
(横坐标与纵坐标均为整数的点称
为整点),使得 为等腰三角形,所有满足条件的点
为等腰三角形,所有满足条件的点 的坐标为 _____________ ;
的坐标为 _____________ ;
(3)将 沿X轴向右平移 个单位时,
沿X轴向右平移 个单位时, 与y轴相切
与y轴相切
相关知识点
推荐套卷
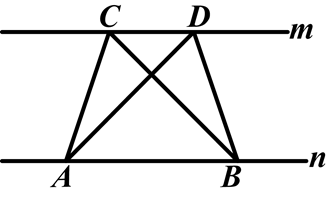
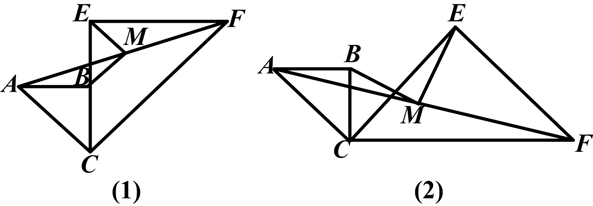
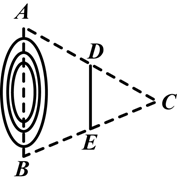
 ,连接DE,CF.
,连接DE,CF.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号