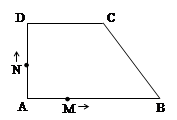已知四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=CD=4,AB=7.
现有M、N两点同时以相同的速度从A点出发,点M沿A—B—C-D方向前进,点N沿A—D—C-B方向前进,直到两点相遇时停止.设点M前进的路程为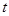 ,△AMN的面积为
,△AMN的面积为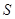 .
.
(1)试确定△AMN存在时,路程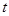 的取值范围.
的取值范围.
(2)请你求出面积S关于路程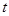 的函数.
的函数.
(3)当点M前进的路程为多少时,△AMN的面积最大?最大是多少?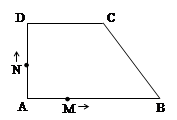


相关知识点
推荐套卷
已知四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=CD=4,AB=7.
现有M、N两点同时以相同的速度从A点出发,点M沿A—B—C-D方向前进,点N沿A—D—C-B方向前进,直到两点相遇时停止.设点M前进的路程为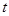 ,△AMN的面积为
,△AMN的面积为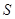 .
.
(1)试确定△AMN存在时,路程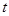 的取值范围.
的取值范围.
(2)请你求出面积S关于路程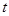 的函数.
的函数.
(3)当点M前进的路程为多少时,△AMN的面积最大?最大是多少?