(本小题满分12分)
已知点R(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上 ,且满足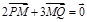 ,
,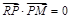 .
.
(Ⅰ)当点P在y轴上移动时,求点M的轨迹C的方程;
(Ⅱ)设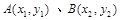 为轨迹C上两点,且
为轨迹C上两点,且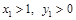 ,N(1,0),求实数
,N(1,0),求实数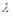 ,使
,使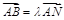 ,且
,且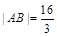 .
.
推荐套卷
(本小题满分12分)
已知点R(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上 ,且满足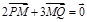 ,
,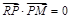 .
.
(Ⅰ)当点P在y轴上移动时,求点M的轨迹C的方程;
(Ⅱ)设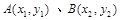 为轨迹C上两点,且
为轨迹C上两点,且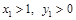 ,N(1,0),求实数
,N(1,0),求实数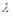 ,使
,使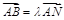 ,且
,且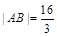 .
.