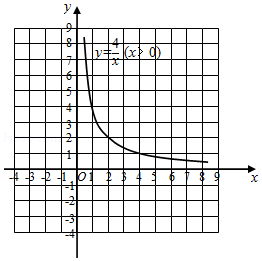
模具厂计划生产面积为4,周长为
的矩形模具.对于
的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为
,
,由矩形的面积为4,得
,即
;由周长为
,得
,即
.满足要求的
应是两个函数图象在第 一 象限内交点的坐标.
(2)画出函数图象
函数
的图象如图所示,而函数
的图象可由直线
平移得到.请在同一直角坐标系中直接画出直线
.
(3)平移直线
,观察函数图象
①当直线平移到与函数
的图象有唯一交点
时,周长
的值为 ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长
的取值范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长
的取值范围为 .