已知⊙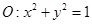 和点
和点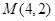 .
.
(Ⅰ)过点 向⊙
向⊙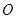 引切线
引切线 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)求以点 为圆心,且被直线
为圆心,且被直线 截得的弦长为4的⊙
截得的弦长为4的⊙ 的方程;
的方程;
(Ⅲ)设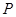 为(Ⅱ)中⊙
为(Ⅱ)中⊙ 上任一点,过点
上任一点,过点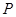 向⊙
向⊙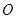 引切线,切点为
引切线,切点为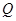 . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点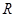 ,使得
,使得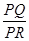 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
推荐套卷
已知⊙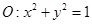 和点
和点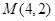 .
.
(Ⅰ)过点 向⊙
向⊙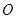 引切线
引切线 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)求以点 为圆心,且被直线
为圆心,且被直线 截得的弦长为4的⊙
截得的弦长为4的⊙ 的方程;
的方程;
(Ⅲ)设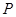 为(Ⅱ)中⊙
为(Ⅱ)中⊙ 上任一点,过点
上任一点,过点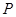 向⊙
向⊙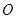 引切线,切点为
引切线,切点为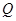 . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点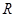 ,使得
,使得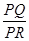 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.