设二次函数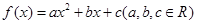 满足下列条件:
满足下列条件:
①当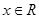 时,
时, 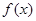 的最小值为0,且
的最小值为0,且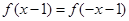 恒成立;
恒成立;
②当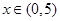 时,
时,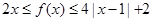 恒成立.
恒成立.
(I)求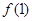 的值;
的值;
(Ⅱ)求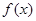 的解析式;
的解析式;
(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当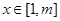 时,就有
时,就有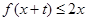 成立
成立
相关知识点
推荐套卷
设二次函数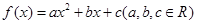 满足下列条件:
满足下列条件:
①当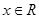 时,
时, 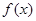 的最小值为0,且
的最小值为0,且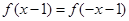 恒成立;
恒成立;
②当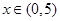 时,
时,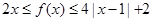 恒成立.
恒成立.
(I)求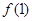 的值;
的值;
(Ⅱ)求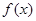 的解析式;
的解析式;
(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当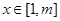 时,就有
时,就有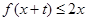 成立
成立