如图,抛物线形的拱桥在正常水位时,水面AB的宽为20m.涨水时水面上升了3m,达到了警戒水位,这时水面宽CD=10m.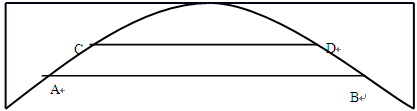
(1)求抛物线的解析式;
(2)当水位继续以每小时0.2m的速度上升时,再经过几小时就到达拱顶?
相关知识点
推荐套卷
如图,抛物线形的拱桥在正常水位时,水面AB的宽为20m.涨水时水面上升了3m,达到了警戒水位,这时水面宽CD=10m.
(1)求抛物线的解析式;
(2)当水位继续以每小时0.2m的速度上升时,再经过几小时就到达拱顶?