某中学举行数学知识竞赛，所有参赛学生分别设有一、二、三等奖和纪念奖，获奖情况已绘制成如图所示的两幅不完整的统计图．根据图中所给出的信息解答下列问题：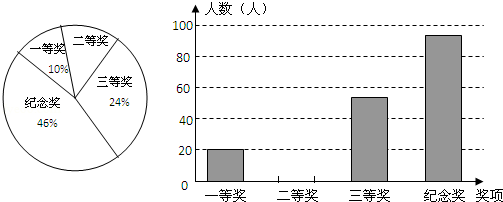
（1）二等奖所占的比例是多少？
（2）这次数学知识竞赛获得二等奖的人数是多少？
（3）请将条形统计图补充完整；
（4）若给所有参赛学生每人发一张卡片，各自写上自己的名字，然后把卡片放入一个不透明的袋子里，摇匀后任意摸出一张，求摸出的卡片上是写有一等奖学生名字的概率．
相关试题
某校组织一项公益知识竞赛，比赛规定：每个班级由2名男生、2名女生及1名班主任老师组成代表队．但参赛时，每班只能有3名队员上场参赛，班主任老师必须参加，另外2名队员分别在2名男生和2名女生中各随机抽出1名．初三（1）班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队，求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率．（请用“画树状图”或“列表”或“列举”等方法给出分析过程）
某汽车交易市场为了解二手轿车的交易情况，将本市场去年成交的二手轿车的全部数据，以二手轿车交易前的使用时间为标准分为 、 、 、 、 五类，并根据这些数据由甲，乙两人分别绘制了下面的两幅统计图（图都不完整）．
请根据以上信息，解答下列问题：
（1）该汽车交易市场去年共交易二手轿车 辆．
（2）把这幅条形统计图补充完整．（画图后请标注相应的数据）
（3）在扇形统计图中， 类二手轿车交易辆数所对应扇形的圆心角为 度．
粤公网安备 44130202000953号