如图，在平面直角坐标系xOy中，已知点B的坐标为（2，0），点C的坐标为（0，8），sin∠CAB=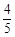
, E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连结CE.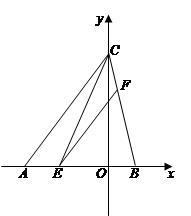
（1）求AC和OA的长；
（2）设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式；
（3）在（2）的条件下试说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．
相关试题
如图1，已知三角形ABC中，AB=BC=1，∠ABC=90度，把一块含30度角的三角板DEF的直角顶点D放在AC的中点上，将直角三角板DEF绕D点按逆时针方向旋转。
（1）在图1中，DE交AB于M，DF交BC于N.
①直接写出DM、DN的数量关系；
②在这一过程中，直角三角板DEF与三角形ABC的重叠部分为四边形DMBN，请说明四边形DMBN的面积是否发生变化？若发生变化，请说明如何变化的；若不发生变化，请求出其面积.
（2）继续旋转至如图2的位置，延长AB交DE于M，延长BC交DF于N，DM=DN是否仍然成立？若成立，请给出证明；若不成立，请说明理由.
，应如何设计每个彩条的宽度？
的方程
，有两个不相等的实数根：
的取值范围；
相关知识点
推荐套卷
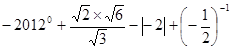粤公网安备 44130202000953号