平面直角坐标系xOy中，抛物线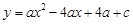
与x轴交于点A、点B，与y轴的正半轴交于点C，点 A的坐标为（1，0），OB=OC，抛物线的顶点为D．
（1）求此抛物线的解析式；
（2）若此抛物线的对称轴上的点P满足∠APB=∠ACB，求点P的坐标；
（3）在（1）的条件下，对于实数c、d，我们可用min{ c，d }表示c、d两数中较小的数，如min{3，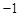
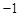}=.若关于x的函数y = min{
，
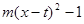
}的图象关于直线
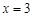对称，试讨论其与动直线
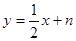交点的个数。
相关试题
用三角尺可按下面方法画角平分线，在已知的∠AOB的两边上，分别取OM=ON，再分别过点M，N作OA、OB的垂线，交点为P，画射线OP，则OP平分∠AOB，为什么？
，这个正多边形是几边形？试根据图中的信息，解答下列问题：
（1）购买6根跳绳需元，购买12根跳绳需元.
（2）小红比小明多买2根，付款时小红反而比小明少5元，你认为有这种可能吗？若有，请求出小红购买跳绳的根数；若没有，请说明理由.
相关知识点
推荐套卷
粤公网安备 44130202000953号