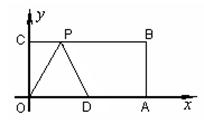
如图1,平面直角坐标系中,抛物线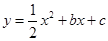 与
与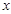 轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与
轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与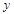 轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
(1)若点F的坐标为(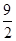 ,
, ),AF=
),AF=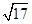 .
.
①求此抛物线的解析式;
②点P是此抛物线上一个动点,点Q在此抛物线的对称轴上,以点A、F、P、Q为顶点构成的四边形是平行四边形,请直接写出点Q的坐标;
(2)若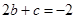 ,
,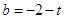 ,且AB的长为
,且AB的长为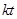 ,其中
,其中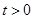 .如图2,当∠DAF=45时,求
.如图2,当∠DAF=45时,求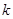 的值和∠DFA的正切值.
的值和∠DFA的正切值.
相关知识点
推荐套卷

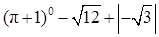

 ,则
,则 的取值范围是
的取值范围是
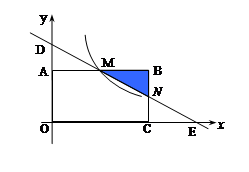
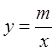 (
(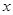 >0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上; (
(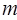 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号