已知矩形ABCD，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．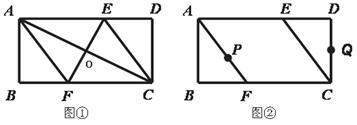
（1）如图①，连接AF、CE，求证四边形AFCE是菱形；
（2）求AF的长；
（3）如图②，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周，即点P自
停止，点Q自
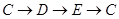停止，在运动过程中：已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动的时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．
相关试题
（本小题6分）已知一次函数y=x+m与反比例函数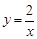
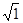
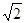
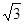
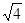
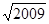的图象在第一象限的交点为P(x0，2).(1) 求x0及m的值；
(2) 求一次函数的图象与两坐标轴的交点坐标..
6分)(1)用“<”，“>”，“＝”填空：
(2)由上可知：①|1－
|=
②|－|=
③|－|= (3)计算(结果保留根号)：
|1－|+|－|+|－|+|－|+…+|
－
|.
(6分)振子从点A开始左右来回振动8次，现规定向右为正，向左为负，这8次振动记录为(单位：毫米)：+10，-9，+8，-6，+7，-6，+8，-7。(1)求振子停止时在A点的哪一侧？距离A点有多远？
(2)如果每毫米需用时0.2秒，则振动这八次共用多少秒？
(8分)(1)如图1，小明想剪一块面积为25cm2的正方形纸板，你能帮他求出正方形纸板的边长吗?
(2)若小明想将两块边长都为3cm的正方形纸板沿对角线剪开，拼成如图2所示的一个大正方形，你能帮他求出这个大正方形的面积吗?它的边长是整数吗?若不是整数，那么请你估计这个边长的值在哪两个整数之间?
相关知识点
推荐套卷
粤公网安备 44130202000953号