若向量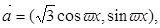
，其中
，记函数
，若函数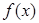
的图象与直线
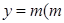为常数）相切，并且切点的横坐标依次成公差为
的等差数列。
（1）求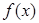的表达式及
的值；
（2）将函数
的图象向左平移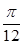
，得到
的图象，当
时，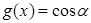
的交点横坐标成等比数列，求钝角
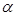的值。
相关试题
的底面为菱形，且∠
，
，
。
平面
；
与平面
所夹角的余弦值．
是正项数列，
，且点
（
）在函数
的图像上．
满足
，
，求证：
．
的弧段上求一点P，使得曲线在该点的切线在y轴上的截距为最小，并求出这个最小值
（
,
,
）的最大值是5，周期为
.
和
的值；（2）若
,
,
，求
的值
，函数
·
，且最小正周期为
．
的值；
，求
的值．相关知识点
推荐套卷
若向量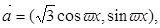，其中，记函数，若函数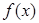的图象与直线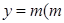为常数）相切，并且切点的横坐标依次成公差为的等差数列。
（1）求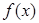的表达式及的值；
（2）将函数的图象向左平移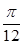，得到的图象，当时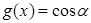，的交点横坐标成等比数列，求钝角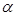的值。
粤公网安备 44130202000953号