如图1，在平面直角坐标系中，直线AB与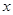
轴交于点A，与
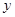轴交于点B，与直线OC：
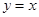交于点C．
（1）若直线AB解析式为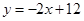
，
①求点C的坐标；
②求△OAC的面积．
（2）如图2，作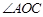
的平分线ON，若AB⊥ON，垂足为E， OA＝4，P、Q分别为线段OA、OE上的动点，连结AQ与PQ，试探索AQ＋PQ是否存在最小值？若存在，求出这个最小值；若不存在，说明理由．
，其中
相关知识点
推荐套卷
如图1，在平面直角坐标系中，直线AB与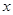轴交于点A，与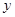轴交于点B，与直线O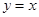C：交于点C．
（1）若直线AB解析式为，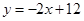
①求点C的坐标；
②求△OAC的面积．
（2）如图2，作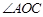的平分线ON，若AB⊥ON，垂足为E， OA＝4，P、Q分别为线段OA、OE上的动点，连结AQ与PQ，试探索AQ＋PQ是否存在最小值？若存在，求出这个最小值；若不存在，说明理由．
粤公网安备 44130202000953号