如图,矩形ABCD中,P是线段AD上一动点,O为BD中点,PO的延长线交BC于Q。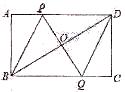
(1)求证:四边形PDQB为平行四边形;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向D运动(不与D重合)。设点P运动时间为t秒,请用t表示PD的长,并求t为何值时,四边形PBQD是菱形。
相关知识点
推荐套卷
如图,矩形ABCD中,P是线段AD上一动点,O为BD中点,PO的延长线交BC于Q。
(1)求证:四边形PDQB为平行四边形;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向D运动(不与D重合)。设点P运动时间为t秒,请用t表示PD的长,并求t为何值时,四边形PBQD是菱形。