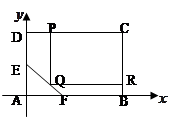为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ//BC,RQ BC。另外
BC。另外 的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?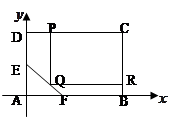
推荐套卷
为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ//BC,RQ BC。另外
BC。另外 的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?