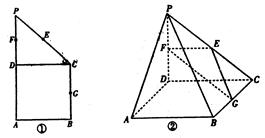
如图①在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD=DC=PD=2，E，F，G分别是线段PC、PD，BC的中点，现将ΔPDC折起，使平面PDC⊥平面ABCD（如图②）
（1）求证AP∥平面EFG；
（2）求二面角G-EF-D的大小；
（3）在线段PB上确定一点Q，使PC⊥平面ADQ，试给出证明。
相关试题
（
为实常数）。
时，证明：
不是奇函数；
与
的值；
.
，且
有最小值2时，求
的值；
时，有
恒成立，求实数
的取值范围.
,q: 
,若
是
的必要不
是定义在（－∞，+∞）上的函数，对一切
均
，且当
时，
，求当
时，推荐套卷
如图①在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD=DC=PD=2，E，F，G分别是线段PC、PD，BC的中点，现将ΔPDC折起，使平面PDC⊥平面ABCD（如图②）
（1）求证AP∥平面EFG；
（2）求二面角G-EF-D的大小；
（3）在线段PB上确定一点Q，使PC⊥平面ADQ，试给出证明。
粤公网安备 44130202000953号