已知圆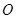 的方程为
的方程为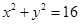 ,过点
,过点 作直线与圆
作直线与圆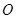 交于
交于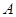 、
、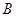 两点。
两点。
(1)若坐标原点O到直线AB的距离为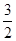 ,求直线AB的方程;
,求直线AB的方程;
(2)当△ 的面积最大时,求直线AB的斜率;
的面积最大时,求直线AB的斜率;
(3)如图所示过点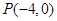 作两条直线与圆O分别交于R、S,若
作两条直线与圆O分别交于R、S,若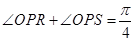 ,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。
,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。
相关知识点
推荐套卷
已知圆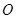 的方程为
的方程为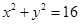 ,过点
,过点 作直线与圆
作直线与圆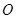 交于
交于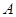 、
、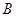 两点。
两点。
(1)若坐标原点O到直线AB的距离为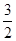 ,求直线AB的方程;
,求直线AB的方程;
(2)当△ 的面积最大时,求直线AB的斜率;
的面积最大时,求直线AB的斜率;
(3)如图所示过点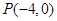 作两条直线与圆O分别交于R、S,若
作两条直线与圆O分别交于R、S,若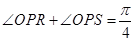 ,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。
,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。