为应对全球经济危机,中国政府投资40000亿元人民币以拉动内需,5月21日国家发改委公布了40000亿元投资构成,具体内容如下:单位:亿元
重 点 投 向
|
资金测算
|
廉租住房等保障性住房
|
4000
|
农村民生工程和基础设施
|
3700
|
铁路等重大基础设施建设和
城市电网改造
|
|
卫生、教育等社会事业发展
|
1500
|
节能减排和生态建设工程
|
2100
|
自主创新和产业结构调整
|
3700
|
汶川地震灾后恢复重建
|
|
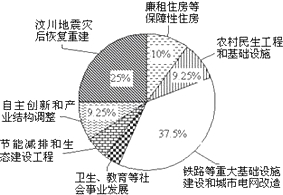
请你根据统计图表中所提供的信息,完成下列问题:
(1)在统计表中,投向“铁路等重大基础设施建设和城市电网改造”的资金测算是 亿元,投向“汶川地震灾后恢复重建”的资金测算是 亿元;
(2)在扇形统计图中,“卫生、教育等社会事业发展”部分所占的百分数是 ,“节能减排和生态建设工程”部分所占的百分数是 ;
(3)统计表“资金测算”栏目下的七个数据中,中位数是 亿元,众数是 亿元;
(4)在扇形统计图中,“廉租住房等保障性住房”部分所占的圆心角为度.