已知定义在实数集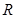
上的奇函数
（
、
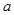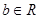）过已知点
．
（Ⅰ）求函数的解析式；
（Ⅱ）试证明函数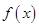
在区间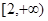
是增函数；若函数
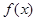在区间
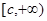（其中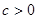
）也是增函数，求
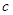的最小值；
（Ⅲ）试讨论这个函数的单调性，并求它的最大值、最小值，在给出的坐标系（见答题卡）中画出能体现主要特征的图简；
（Ⅳ）求不等式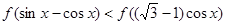
的解集．
相关试题
在（0，1）内是增函数.
的取值范围;
，求证：
.
的首项
，前
项和为
，满足关系
（
,
,3,4…）
，作数列
，使
，
.（
…
的值
（
）
的定义域；
、
，当
时，
，且
若存在，求出
（
，
）
的值域；
，且
的最小值为
，求
满足：当
时，
，
时，
时，
的表达式；
满足什么条件时，函数
有4个零点，相关知识点
推荐套卷
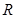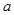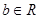已知定义在实数集上的奇函数（、）过已知点．
（Ⅰ）求函数的解析式；
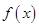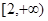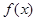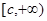（Ⅱ）试证明函数在区间是增函数；若函数在区间（其中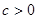）也是增函数，求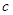的最小值；
（Ⅲ）试讨论这个函数的单调性，并求它的最大值、最小值，在给出的坐标系（见答题卡）中画出能体现主要特征的图简；
（Ⅳ）求不等式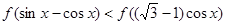的解集．
粤公网安备 44130202000953号